Show The 20 Bits Key Stream Generated From
In a stream cipher structure a key is input to a pseudorandom bit generator that produces a stream of 8-bit numbers that are apparently random. The output of the generator, called a , is combined one byte at a time with the plaintext stream using the bitwise exclusive-OR operation. A stream cipher makes use of a much smaller and more convenient key such as 128 bits. Based on this key, it generates a pseudorandom keystream which can be combined with the plaintext digits in a similar fashion to the one-time pad. However, this comes at a cost. The keystream is now pseudorandom and so is not truly random.
- Show The 20 Bits Key Stream Generated From The Internet
- Show The 20 Bits Key Stream Generated From One
For reference, this article details the various tables referenced in the Data Encryption Standard (DES)block cipher.
All bits and bytes are arranged in big endian order in this document. That is, bit number 1 is always the most significant bit.
Initial permutation (IP)[edit]
| 58 | 50 | 42 | 34 | 26 | 18 | 10 | 2 |
| 60 | 52 | 44 | 36 | 28 | 20 | 12 | 4 |
| 62 | 54 | 46 | 38 | 30 | 22 | 14 | 6 |
| 64 | 56 | 48 | 40 | 32 | 24 | 16 | 8 |
| 57 | 49 | 41 | 33 | 25 | 17 | 9 | 1 |
| 59 | 51 | 43 | 35 | 27 | 19 | 11 | 3 |
| 61 | 53 | 45 | 37 | 29 | 21 | 13 | 5 |
| 63 | 55 | 47 | 39 | 31 | 23 | 15 | 7 |
This table specifies the input permutation on a 64-bit block. /visualizerexe-key-generator-artios-14.html. The meaning is as follows: the first bit of the output is taken from the 58th bit of the input; the second bit from the 50th bit, and so on, with the last bit of the output taken from the 7th bit of the input.
This information is presented as a table for ease of presentation; it is a vector, not a matrix.
Final permutation (IP−1)[edit]
| 40 | 8 | 48 | 16 | 56 | 24 | 64 | 32 |
| 39 | 7 | 47 | 15 | 55 | 23 | 63 | 31 |
| 38 | 6 | 46 | 14 | 54 | 22 | 62 | 30 |
| 37 | 5 | 45 | 13 | 53 | 21 | 61 | 29 |
| 36 | 4 | 44 | 12 | 52 | 20 | 60 | 28 |
| 35 | 3 | 43 | 11 | 51 | 19 | 59 | 27 |
| 34 | 2 | 42 | 10 | 50 | 18 | 58 | 26 |
| 33 | 1 | 41 | 9 | 49 | 17 | 57 | 25 |
The final permutation is the inverse of the initial permutation; the table is interpreted similarly.
Expansion function (E)[edit]
| 32 | 1 | 2 | 3 | 4 | 5 |
| 4 | 5 | 6 | 7 | 8 | 9 |
| 8 | 9 | 10 | 11 | 12 | 13 |
| 12 | 13 | 14 | 15 | 16 | 17 |
| 16 | 17 | 18 | 19 | 20 | 21 |
| 20 | 21 | 22 | 23 | 24 | 25 |
| 24 | 25 | 26 | 27 | 28 | 29 |
| 28 | 29 | 30 | 31 | 32 | 1 |
The expansion function is interpreted as for the initial and final permutations. Note that some bits from the input are duplicated at the output; e.g. the fifth bit of the input is duplicated in both the sixth and eighth bit of the output. Thus, the 32-bit half-block is expanded to 48 bits.
Permutation (P)[edit]
| 16 | 7 | 20 | 21 | 29 | 12 | 28 | 17 |
| 1 | 15 | 23 | 26 | 5 | 18 | 31 | 10 |
| 2 | 8 | 24 | 14 | 32 | 27 | 3 | 9 |
| 19 | 13 | 30 | 6 | 22 | 11 | 4 | 25 |
The P permutation shuffles the bits of a 32-bit half-block.
Permuted choice 1 (PC-1)[edit]
|
|
The 'Left' and 'Right' halves of the table show which bits from the input key form the left and right sections of the key schedule state. Note that only 56 bits of the 64 bits of the input are selected; the remaining eight (8, 16, 24, 32, 40, 48, 56, 64) were specified for use as parity bits.
Permuted choice 2 (PC-2)[edit]
| 14 | 17 | 11 | 24 | 1 | 5 |
| 3 | 28 | 15 | 6 | 21 | 10 |
| 23 | 19 | 12 | 4 | 26 | 8 |
| 16 | 7 | 27 | 20 | 13 | 2 |
| 41 | 52 | 31 | 37 | 47 | 55 |
| 30 | 40 | 51 | 45 | 33 | 48 |
| 44 | 49 | 39 | 56 | 34 | 53 |
| 46 | 42 | 50 | 36 | 29 | 32 |
This permutation selects the 48-bit subkey for each round from the 56-bit key-schedule state. This permutation will ignore 8 bits below:
Permuted Choice 2 'PC-2' Ignored bits 9,18,22,25,35,38,43,54.
Substitution boxes (S-boxes)[edit]
| S1 | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0yyyy0 | 14 | 4 | 13 | 1 | 2 | 15 | 11 | 8 | 3 | 10 | 6 | 12 | 5 | 9 | 0 | 7 |
| 0yyyy1 | 0 | 15 | 7 | 4 | 14 | 2 | 13 | 1 | 10 | 6 | 12 | 11 | 9 | 5 | 3 | 8 |
| 1yyyy0 | 4 | 1 | 14 | 8 | 13 | 6 | 2 | 11 | 15 | 12 | 9 | 7 | 3 | 10 | 5 | 0 |
| 1yyyy1 | 15 | 12 | 8 | 2 | 4 | 9 | 1 | 7 | 5 | 11 | 3 | 14 | 10 | 0 | 6 | 13 |
| S2 | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x |
| 0yyyy0 | 15 | 1 | 8 | 14 | 6 | 11 | 3 | 4 | 9 | 7 | 2 | 13 | 12 | 0 | 5 | 10 |
| 0yyyy1 | 3 | 13 | 4 | 7 | 15 | 2 | 8 | 14 | 12 | 0 | 1 | 10 | 6 | 9 | 11 | 5 |
| 1yyyy0 | 0 | 14 | 7 | 11 | 10 | 4 | 13 | 1 | 5 | 8 | 12 | 6 | 9 | 3 | 2 | 15 |
| 1yyyy1 | 13 | 8 | 10 | 1 | 3 | 15 | 4 | 2 | 11 | 6 | 7 | 12 | 0 | 5 | 14 | 9 |
| S3 | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x |
| 0yyyy0 | 10 | 0 | 9 | 14 | 6 | 3 | 15 | 5 | 1 | 13 | 12 | 7 | 11 | 4 | 2 | 8 |
| 0yyyy1 | 13 | 7 | 0 | 9 | 3 | 4 | 6 | 10 | 2 | 8 | 5 | 14 | 12 | 11 | 15 | 1 |
| 1yyyy0 | 13 | 6 | 4 | 9 | 8 | 15 | 3 | 0 | 11 | 1 | 2 | 12 | 5 | 10 | 14 | 7 |
| 1yyyy1 | 1 | 10 | 13 | 0 | 6 | 9 | 8 | 7 | 4 | 15 | 14 | 3 | 11 | 5 | 2 | 12 |
| S4 | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x |
| 0yyyy0 | 7 | 13 | 14 | 3 | 0 | 6 | 9 | 10 | 1 | 2 | 8 | 5 | 11 | 12 | 4 | 15 |
| 0yyyy1 | 13 | 8 | 11 | 5 | 6 | 15 | 0 | 3 | 4 | 7 | 2 | 12 | 1 | 10 | 14 | 9 |
| 1yyyy0 | 10 | 6 | 9 | 0 | 12 | 11 | 7 | 13 | 15 | 1 | 3 | 14 | 5 | 2 | 8 | 4 |
| 1yyyy1 | 3 | 15 | 0 | 6 | 10 | 1 | 13 | 8 | 9 | 4 | 5 | 11 | 12 | 7 | 2 | 14 |
| S5 | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x |
| 0yyyy0 | 2 | 12 | 4 | 1 | 7 | 10 | 11 | 6 | 8 | 5 | 3 | 15 | 13 | 0 | 14 | 9 |
| 0yyyy1 | 14 | 11 | 2 | 12 | 4 | 7 | 13 | 1 | 5 | 0 | 15 | 10 | 3 | 9 | 8 | 6 |
| 1yyyy0 | 4 | 2 | 1 | 11 | 10 | 13 | 7 | 8 | 15 | 9 | 12 | 5 | 6 | 3 | 0 | 14 |
| 1yyyy1 | 11 | 8 | 12 | 7 | 1 | 14 | 2 | 13 | 6 | 15 | 0 | 9 | 10 | 4 | 5 | 3 |
| S6 | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x |
| 0yyyy0 | 12 | 1 | 10 | 15 | 9 | 2 | 6 | 8 | 0 | 13 | 3 | 4 | 14 | 7 | 5 | 11 |
| 0yyyy1 | 10 | 15 | 4 | 2 | 7 | 12 | 9 | 5 | 6 | 1 | 13 | 14 | 0 | 11 | 3 | 8 |
| 1yyyy0 | 9 | 14 | 15 | 5 | 2 | 8 | 12 | 3 | 7 | 0 | 4 | 10 | 1 | 13 | 11 | 6 |
| 1yyyy1 | 4 | 3 | 2 | 12 | 9 | 5 | 15 | 10 | 11 | 14 | 1 | 7 | 6 | 0 | 8 | 13 |
| S7 | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x |
| 0yyyy0 | 4 | 11 | 2 | 14 | 15 | 0 | 8 | 13 | 3 | 12 | 9 | 7 | 5 | 10 | 6 | 1 |
| 0yyyy1 | 13 | 0 | 11 | 7 | 4 | 9 | 1 | 10 | 14 | 3 | 5 | 12 | 2 | 15 | 8 | 6 |
| 1yyyy0 | 1 | 4 | 11 | 13 | 12 | 3 | 7 | 14 | 10 | 15 | 6 | 8 | 0 | 5 | 9 | 2 |
| 1yyyy1 | 6 | 11 | 13 | 8 | 1 | 4 | 10 | 7 | 9 | 5 | 0 | 15 | 14 | 2 | 3 | 12 |
| S8 | x0000x | x0001x | x0010x | x0011x | x0100x | x0101x | x0110x | x0111x | x1000x | x1001x | x1010x | x1011x | x1100x | x1101x | x1110x | x1111x |
| 0yyyy0 | 13 | 2 | 8 | 4 | 6 | 15 | 11 | 1 | 10 | 9 | 3 | 14 | 5 | 0 | 12 | 7 |
| 0yyyy1 | 1 | 15 | 13 | 8 | 10 | 3 | 7 | 4 | 12 | 5 | 6 | 11 | 0 | 14 | 9 | 2 |
| 1yyyy0 | 7 | 11 | 4 | 1 | 9 | 12 | 14 | 2 | 0 | 6 | 10 | 13 | 15 | 3 | 5 | 8 |
| 1yyyy1 | 2 | 1 | 14 | 7 | 4 | 10 | 8 | 13 | 15 | 12 | 9 | 0 | 3 | 5 | 6 | 11 |
Show The 20 Bits Key Stream Generated From The Internet
This table lists the eight S-boxes used in DES. Each S-box replaces a 6-bit input with a 4-bit output. Given a 6-bit input, the 4-bit output is found by selecting the row using the outer two bits, and the column using the inner four bits. For example, an input '011011' has outer bits '01' and inner bits '1101'; noting that the first row is '00' and the first column is '0000', the corresponding output for S-box S5 would be '1001' (=9), the value in the second row, 14th column. (See S-box).
Key Generation[edit]
The main key supplied from user is of 64 bits. The following operations are performed with it.
Drop Parity bits[edit]
Drop the bits of the grey positions (8x) to make 56 bit space for further operation for each round.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 |
| 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 |
| 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 |
After that bits are permuted according to the following table,
The table is row major way, means,
Actual Bit position = Substitute with the bit of row * 8 + column.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| 1 | 57 | 49 | 41 | 33 | 25 | 17 | 9 | 1 |
| 2 | 58 | 50 | 42 | 34 | 26 | 18 | 10 | 2 |
| 3 | 59 | 51 | 43 | 35 | 27 | 19 | 11 | 3 |
| 4 | 60 | 52 | 44 | 36 | 63 | 55 | 47 | 39 |
| 5 | 31 | 23 | 15 | 7 | 62 | 54 | 46 | 38 |
| 6 | 30 | 22 | 14 | 6 | 61 | 53 | 45 | 37 |
| 7 | 29 | 21 | 13 | 5 | 28 | 20 | 12 | 4 |
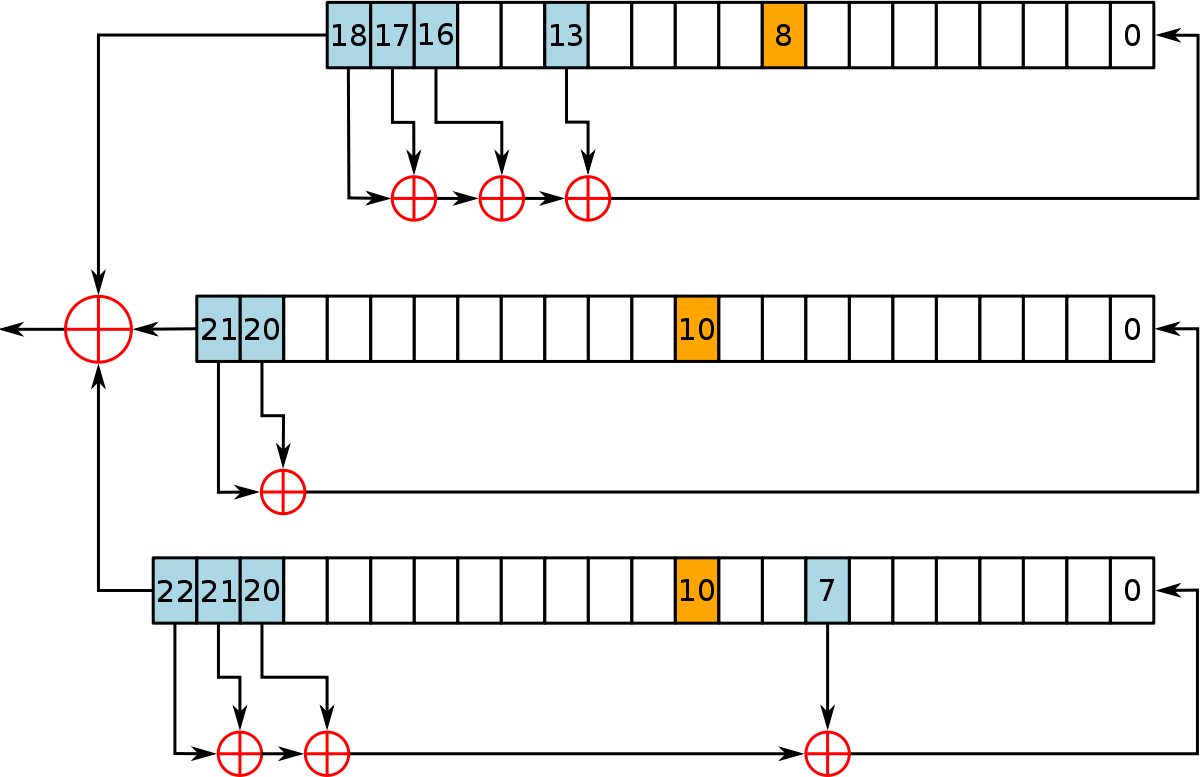
Bits Rotation[edit]
Before the round sub-key is selected, each half of the key schedule state is rotated left by a number of places. This table specifies the number of places rotated.
• The key is divided into two 28-bit parts
• Each part is shifted left (circular) one or two bits
• After shifting, two parts are then combined to form a 56 bit temp-key again
| Number of Round | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of Left rotations | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 |
Show The 20 Bits Key Stream Generated From One
Key Compression[edit]
• The compression P-box changes the 56 bits key to 48 bits key, which is used as a key for the corresponding round.
The table is row major way, means,
Actual Bit position = Substitute with the bit of row * 8 + column.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| 1 | 14 | 17 | 11 | 24 | 01 | 05 | 03 | 28 |
| 2 | 15 | 06 | 21 | 10 | 23 | 19 | 12 | 04 |
| 3 | 26 | 08 | 16 | 07 | 27 | 20 | 13 | 02 |
| 4 | 41 | 52 | 31 | 37 | 47 | 55 | 30 | 40 |
| 5 | 51 | 45 | 33 | 48 | 44 | 49 | 39 | 56 |
| 6 | 34 | 53 | 46 | 42 | 50 | 36 | 29 | 32 |
After this return the Round-Key of 48 bits to the called function, i.e. the Round.
References[edit]
- Data Encryption Standard (DES)(PDF). National Institute of Standards and Technology (NIST). 1999-10-25. FIPS PUB 46-3.
External links[edit]
Description
Pseudorandom numbers in MATLAB® come from one or more randomnumber streams. The simplest way to generate arrays of random numbersis to use rand, randn, or randi.These functions all rely on the same stream of uniform random numbers,known as the global stream. You can createother streams that act separately from the global stream, and youcan use their rand, randi, or randn methodsto generate arrays of random numbers. You can also create a randomnumber stream and make it the global stream.
To create a single random number stream, use the RandStream constructor.To create multiple independent random number streams, use RandStream.create.The rng function provides asimple interface to create a new global stream.
stream = RandStream.getGlobalStream returnsthe global random number stream, that is, the one currently used bythe rand, randi, and randn functions.
prevstream = RandStream.setGlobalStream(stream) designatesthe random number stream stream as the new globalstream to be used by the rand, randi, and randn functions,and returns the previous global stream.
A random number stream s has propertiesthat control its behavior. Access or assign to a property using p= s.Property or s.Property = p. The followingtable lists defined properties: